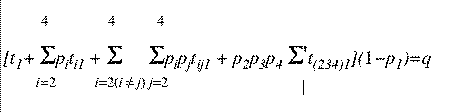
Brian Meek is now at King's College London.
With some differences in presentation, the paper was originally published in French in Mathématiques et Sciences Humaines, No 25, pp13-23, 1969.
Candidates with more than q votes are elected, and have their surplus votes transferred according to the next preferences marked; if there are no such candidates, the bottom candidate is eliminated and all his votes so transferred. Repeated application of these rules ensures that at the end of the count s candidates have at least q votes each and so the total wasted vote w satisfies w < T/(s+1).
Given s and T, it is clear from the definition of q
that condition (A) is satisfied provided the next preference at each
transfer is always given. It is possible for the above inequality, and hence
condition (A), to be violated, if w is increased by the addition of
votes which are non-transferable because no next preference has been
indicated. In this paper we shall assume that this does not occur; it will
be shown in a second paper that it is possible still to satisfy (A) in such
cases by modifying the definition of q.
3. Equality of treatment
The discussion of condition (A) shows that, in general, there will be some
wasted votes, except in the trivial cases when s >= T.
It is therefore not possible under STV to guarantee that all
votes will be taken equally into account (e.g. votes with first preferences
for runner-up candidates), although all are taken indirectly into account
when calculating the quota.[2]
Within this obvious limitation, attempts have been made to eliminate possible sources of inequity of treatment by various modifications of the counting rules. Such sources include:
Difficulty (1) is overcome by transferring the appropriate proportion of each divided vote, while the method clearly reduces the errors involved in (2) by the factor 1/K. If K=10**n this is simply working to n decimal places. The value of K has only to be increased until the errors are too small to affect the result of the election.[3] The method is equivalent to transferring the whole vote at an appropriately reduced value, and it is this interpretation we shall use from now on.
Difficulty (3) is slightly more technical, and warrants further explanation. Suppose at some stage a candidate has obtained x (<q) votes. By transfer from another (elected or eliminated) candidate he now acquires a further y votes, where x+y >= q. His surplus is now z=x+y-q. It would appear that his x+y votes should now be transferred, with value reduced by the factor z/(x+y).
It is, however, common practice for only the y votes to be transferred, with value reduced by the factor z/y. The reason for adopting this procedure is simply the practical one, in a manual count, of reducing as much as possible the rescrutiny of ballots for later preferences. However, neither this nor the argument that 'the difference is unlikely to affect the result' are particularly relevant to a decision-theoretic discussion, though we shall return to the practicability problem later.
Of more importance here is the argument 'in STV a vote only counts for one candidate at a time, and should count for the first preference where possible'. If accepted, this would of course also render difficulties (i) and (ii) irrelevant, and the Senate Rules unnecessary; the first part of it is in fact sometimes used as a 'proof' that STV satisfies condition (B). But even without the Senate Rules the statement is false; however the surplus votes are chosen for transfer, it is the existence of the untransferred votes which makes the transferred votes surplus. A vote not only counts directly for one candidate; it can indirectly affect the progress of the count, the pattern of transfers, and ultimately the election or non-election of other candidates.[4]
It is this fact which is at the root of the failure of STV to satisfy condition (B).
In the specific situation described above, the candidate achieves election not only because of the accession of the y new votes, but because of the existence of the x previous votes; hence for condition (B) to be satisfied, all x+y votes should be transferred at the appropriate reduced value.
However, there is yet a fourth difficulty, one which does not seem to have been recognised hitherto.
Let us suppose that of y votes to be transferred, y/2 are marked next to go to candidate A, and y/2 to candidate B. Let us further suppose that A has already been elected; under STV the y/2 votes which would otherwise go to him are transferred to the next candidate marked (assumed C in every case) provided that that candidate is not also already elected. Thus y/2 go to B, and y/2 to C. The inequities are plain; the votes for A which enabled the y/2 to go to C rather than A had no say in their destination, while C obtains these votes at the same value as B receives his. Suppose these y votes were originally first-preference votes for a candidate D, now eliminated; those who voted for A next and then C at least have had their second choice elected, while those who voted next for B have not - yet these votes go, under STV, to both B and C at full value.
In section 6 we shall describe a counting mechanism which overcomes all these difficulties.
Let T=3599, s=3, q=900, and the unsophisticated first-preference votes for the six candidates A, B, ... F be as follows:
A B C D E F
1020 890 880 589 200 20
In this case the 120 surplus votes of A divide 60 to B, 20 to C, 40 to D and
the elected candidates are A, B and C.
Suppose there are 170 voters who above voted A, D, C ... It is known that the second-preference votes of F will go to C, and of E to D. Then the sophisticated way for these 170 to vote is F, A, D, C,... in order to prevent A from being elected on the first count.
A B C D E F
850 890 880 589 200 190
On the elimination of F, his original 20 votes go to C, and the 170
sophisticated votes return to A. However, the 120 surplus is now taken
entirely from this batch (see (3) in section 3) and goes
to D. C having no surplus, E must be eliminated and D is elected.
A different type of sophisticated voting is given below: T=239, s=2, q=80.
Unsophisticated case: C and A elected:
C,A,B... C,B,A... B,A.... A,B.....
120 80 31 8
Sophisticated case: C and B elected:
C,A,B... C,B,A... E,B,A... B,A.... A,B.....
120 50 30 31 8
It seems to be a new result that sophisticated voting is possible in STV,
though it is well-known that it can occur in other voting systems and
considerable work has been done on decision processes using a
games-theoretic approach. Black [5] in his discussion of
STV does mention the possibility of 'an organised minority (perverting) the
use of the system' but only in connection with a candidate with just the
quota on first preferences who is rated last by the rest of the electorate.
STV supporters would claim that if a candidate can obtain a quota this
ipso facto entitles him to be elected, particularly if he gets the
quota on first preferences, and it is certainly difficult to understand what
Black means by 'pervert' in this context.
The conditions (A), (B), (C) discussed so far were chosen simply because they seem to be specific to STV among constituency-type systems in parliamentary elections. However, other conditions could be applied, notably those specified by Arrow in his General Possibility Theorem.[6]
As STV elections are multi-vacancy, the preferences between candidates listed by the voters do not as they stand represent an ordering of independent alternatives, and so Arrow's analysis is not directly applicable. The deduction from the voter's ordering of candidates of his ordering of the actual independent alternatives (the possible subsets of the set of all candidates who might actually be elected) is by no means straightforward. Nevertheless, at some stage of the count the process reduces to electing one candidate to one remaining vacancy, and so the consequences of the theorem, and the Condorcet paradox, cannot be escaped. Using the alternatives as they stand, even though they are not independent, STV clearly satisfies Arrow's conditions 1, 4, and 5. The condition 3 of independence of irrelevant alternatives is not satisfied, nor is condition 2 (the positive association of social and individual values). This can be seen from the above analysis.
A related point, and probably the strongest decision-theoretic argument against STV, is the fact that a candidate may be everyone's second choice but not be elected. This difficulty is not overcome by the feedback method, and it does not seem to the author to be possible to do so while retaining a system which would be recognisably a 'single' transferable vote.
Virtually all other discussion of STV, both for and against, seem to have been about political and not decision-theoretic considerations.
For example, Black[5] does discuss STV from what he terms
the 'statical' point of view, but although he does express some disquiet
about the 'heterogeneity' involved in STV (basically, that some votes count
for first preferences, others for second or later preferences), he does not
go into the problem in detail and concludes 'in spite of those drawbacks
(STV) has merits ... it is not difficult to see why many people,
regarding it purely as a statical system, (Black's italics) should
hold (it) in esteem'. The italicised phrase is to introduce other,
'dynamical' arguments against STV.[7] Black does not discuss
the conditions mentioned here; though the germ of the idea of inequity is
contained in the word 'heterogeneity'; in fact as section
3 shows, the heterogeneity which worries him is more apparent than real,
and the feedback method described in section 6 eliminates
what there is. Nor - oddly - does the 'everyone's second choice' problem,
even though this is closely connected with the doubts mentioned at the end
of the last section.
6. The feedback process
One of the criticisms of STV which is often made is that its rules are too
complicated, and are not derived from principles which can be simply stated.
The above discussion shows that this is not surprising; the rules are in
many cases little more than rules of thumb, designed for practical
convenience rather than theoretic merit. The feedback process, however, is
derived from simply-stated principles:
Note that the proportion of each of B's votes to be transferred is increased by this accession of support; B's supporters have a say in the transfer of the extra surplus, since it is their existence which has made it surplus. All support for B is now treated equally, being divided proportionately to leave him with exactly the quota.
Consider now the effect of Principle 2. The transfer of B's vote may lead to another candidate, D, being elected. All votes, new and old, for D, have now to be divided, leaving D with the quota and distributing the rest to the next non-eliminated candidate. Some ballots may have B, another elected candidate, as next candidate. Under previous rules, only continuing (i.e. non-eliminated and non-elected) candidates can receive transfers. Now these votes are regarded as extra support for B: he takes the proportion allotted him by D, retains the proportion that he keeps of all he receives, and transfers the rest - now the third marked candidate. Formerly the third candidate would get all of the proportion transferred by D (see (iv) section 3).
It can be seen that B will once more have more than the quota if he does not again reduce the proportion which he retains. However, the increased proportion transferred may in part go to D who will therefore have to reduce the proportion he retains. This will react back on B, and it is clear that we have an infinite regression. However, it is also clear that the proportions for transfer do not increase without limit, there being only a finite total surplus available from B and D, who must each retain a quota. The problem is in fact a mathematical one of determining the proportions to be retained by each which will leave them both with a quota, taking into account the extent of mutual support. If pB is the proportion B transfers, and pD that which D transfers, supporters of both B and D have their votes transferred to third preferences at value pB×pD. Those putting B first have 1-pB retained by him and pB×(1-pD) retained by D; those putting D first have 1-pD retained by him and pD×(1-pB) retained by B.
We now, as examples, give the formulae for the proportions for transfer in the cases of 1, 2, 3 and 4 elected candidates:
This is the same formula as before, except that t1 now contains all effective first-preference votes for the candidate, including those obtained from eliminated candidates, who by Principle 1 are now ignored. The proportion p1 is recalculated every time t1 is increased by the elimination of a candidate.
(t1+p2×t21)(1-p1)=q
(t2+p1×t12)(1-p2)=q
Thus:
[t1+p2×t21+p3×t31+p2×p3(t321+t231)](1-p1)=q
Two similar formulae hold, obtained by cyclic permutation of the suffices.
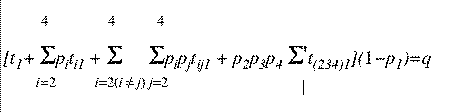
where dashed summation indicates summation over all permutations of (234); there are three similar formulae.
The extension to any number of candidates is straightforward. It should be noted:
The total vote for the two candidates is t1+t2; for them both to be elected t1+t2 >= 2q. Suppose the strict inequality holds; in a non-trivial case t12, t21 are both non-zero. Further, at least one of t1, t2 is greater than q; assume it is t1. If we put p2=0 in (1) we can solve for p1, giving a value p1 > 0. This p1 is the proportion to be transferred if candidate 1 were the only elected candidate; thus t2+p1×t12 > q or candidate 2 would not be elected. If the equality holds, candidate 2 only just gets the quota and so p2=0 from equation (2); thus the equations are solved.
If the strict inequality holds, we get a value of p2 > 0 which is too small. Substituting in (1) increases the coefficient of (1-p1) and hence increases p1; the new value of p1 is increased (but is still too low). Substitution in (2) gives similarly an increased, but too low, value of p2. Thus the iterative process gives monotonically increasing sequences of values p1, p2 bounded above, which hence tend to limits which are the solutions of the equations. A cycle of iterations which leads to two successive sets of values the same to the given accuracy is taken as the approximate solution required. Note that the approximate values may be slightly smaller than the exact ones, but this is exactly what we want; otherwise too much of the support for the candidate concerned would be transferred and he would be left with less than the quota. The process can also be easily shown to work in the limiting case, t1+t2=2q.
It is clear that the success of this iterative procedure depends on the fact that all the quantities in the totals (the coefficients of (1-pi) in each equation) are non-negative, and that therefore it will work for any number of equations provided they are solved cyclically in order of election - this condition being necessary to avoid getting negative values of pi. Since the counting process can only increase the totals of support for elected candidates, it is also clear that the pi for those candidates can only increase as the count progresses;[10] thus it is safe to take as starting values of the pi the ones obtained at a previous stage, putting pi=0 initially for newly-elected candidates only (in which case, as mentioned above, the equations reduce to the ones at the previous stage and hence will yield, at the beginning of the iteration, the same answers).
It can be shown fairly simply that the convergence rate of the iterative process is likely to be unsatisfactory only when both of the following conditions hold; that all the pi are small, and the cross-totals tij etc, are as large as possible. This would not cause difficulty even on the rare occasions on which all these conditions were satisfied, since the occurrence of slow convergence can be detected in advance and allowed for, while at a later stage in the count some at least of the pi are likely to rise sufficiently to accelerate to the true convergence satisfactorily.
It may be argued that the actual results of any election would be different so infrequently that the additional complication is unnecessary. This is a matter for conjecture, or preferably, for further investigation. However, the method has been tried out in two cases, once using figures obtained by a quasi-random process, and once in an actual STV election. In both, there were differences in the candidates elected.[12] Particularly since STV supporters lay such emphasis on the criterion of equality of treatment (condition (B)), it would seem worthwhile in automated counting to adopt the feedback method.
To sum up, the feedback method does satisfy the criterion, subject to the limitations imposed by the basic STV system - i.e. the theoretical minimum of wasted votes, and the elimination of candidates. There is one further limitation not so far discussed, imposed by the voters themselves if they take advantage of the possibility allowed by STV of listing only some of the candidates in preference order. The extension of the feedback method to cover this is dealt with in Paper II; it turns out that the extension also, as a bonus, allows voters to express their views much more accurately than under previous STV methods.[13]